Reactor por lotes

Un reactor por lotes de mezcla completa es espacialmente homogéneo como resultado de una agitación intensa; la temperatura y el pH también pueden mantenerse uniformes, en todo punto del reactor, con un control apropiado.

La forma más general de las ecuaciones de balance de materiales y de energía para las especies de interés, es:

1.

Donde:

V es el volumen del reactor;

c_i es la concentración del componente i ;

c_j representa la concentración de otras especies que pueden influir las velocidades de formación o consumo de i en la reacción y

r(c_i, c_j) es la velocidad volumétrica de formación de c_i por la reacción.

También se puede escribir un balance de masa global para el sistema:

2.

Suponiendo que la densidad total de la fase líquida ( r ) es constante, el volumen de líquido permanece constante, y se puede sacar V del diferencial de la ecuación anterior, para obtener:

3.

Con la densidad ( r ), y las capacidades caloríficas constantes, la ecuación de conservación de la energía se puede escribir como:

4.

Donde:

c_p es la capacidad calorífica;

D H_R es el calor de reacción y

r_X es la velocidad volumétrica del incremento en la masa de células secas.

Aunque el biorreactor se opera por lotes, la ecuación de balance de energía contiene los términos para el flujo de calor del reactor asociado con el control de la temperatura (Q ) y para la generación de calor por agitación (-W, trabajo de eje).

Como ejemplo, el crecimiento microbial puede representarse por dos ecuaciones para la masa de células y el sustrato, utilizando el modelo de Monod:

5.

6.

Con condiciones iniciales X(0) = X₀ ; c_S(0) = c_S0

Estas ecuaciones pueden sumarse después de multiplicar la ecuación 6 por Y_X/S para obtener:

Y de esta forma:

7.

Expresando X en función de c_S , a partir de la ecuación anterior y reemplazando el resultado en la ecuación 6, se tiene:

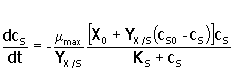8.

Ecuación que puede integrarse analíticamente para obtener:

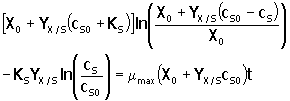9.

En esta ecuación, c_S está implícita y el tiempo en el cual se consume el sustrato, puede encontrarse calculando valores de t correspondientes a valores específicos de la concentración de sustrato.

Si en el cultivo se forma un producto que puede estar parcialmente asociado o no asociado al crecimiento microbial, de la forma:

10.

el balance de materiales para el sustrato debe reescribirse para contabilizar la conversión de sustrato en producto, (ecuación 11), y las tres ecuaciones de balance de material que resultan: ecuaciones 5, 10 y 11, pueden resolverse numéricamente para obtener los perfiles de concentración típicos.

11.

Muerte de células en un cultivo por lotes

En un cultivo en crecimiento, algunas células pueden volverse inactivas o morir, como resultado de errores en la autosíntesis (mala interpretación del ADN, por ejemplo). No obstante la fracción de células viables en los cultivos bacteriales puede ser bastante alta en el crecimiento por lotes, las células eucariotes pueden morir a velocidades apreciables, y así, la viabilidad de ese cultivo será menor del 100%. Si se considera que únicamente las células viables ( X_v ) generan células no viables ( X_nv ) con una cinética de primer orden, en función de la concentración de células viables con una constante de velocidad de reacción k , se tiene, para el crecimiento microbial:

12.

13.

El crecimiento de la población total de células está dado por:

14.

Si se considera que m es aproximadamente constante para la mayor parte de la fase exponencial del crecimiento por lotes, la ecuación 12 puede integrarse para X_v (t ) y el resultado se sustituye en la ecuación 14 para X_T . La integración de la ecuación que resulta, proporciona la concentración de células viables y la relación de viabilidad (X_v /X_T):

15.

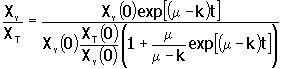16.

Si el inóculo se compone principalmente de células viables, X_v(0)/X_T(0) es aproximadamente igual a 1, y la expresión para la viabilidad, se reduce para tiempos lo suficientemente grandes (exp(m - k)t >1) a:

17.

esto es, la viabilidad fraccional permanece constante para la mayor parte del período exponencial de crecimiento. Si la velocidad de muerte k es igual a la velocidad de crecimiento, m , se tiene entonces un crecimiento lineal de la biomasa total:

18.