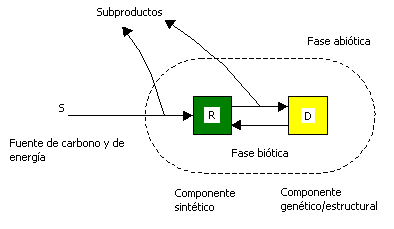
Obtención de un modelo estructurado intrínseco en estado estable
Afortunadamente, el deseo de simular con más precisión la complicada cinética de crecimiento y la de la síntesis de producto de organismos unicelulares, ha conducido al reciente desarrollo de modelos menos fenomenológicos y más realísticos, para sustituir a aquellos basados en la cinética enzimática de Michaelis – Menten (el ejemplo más claro, la ecuación de Monod). Los modelos intrínsecos estructurados son particularmente mejores para aplicaciones complejas como estas descripciones multi – variables de biomasa; son más flexibles que los modelos no estructurados y proveen una distinción más clara entre la biomasa inmovilizada y los alrededores del microambiente.
Esener et al. desarrolló un modelo estructurado que describe la biomasa por medio de dos variables bióticas intrínsecas. El componente R consiste principalmente de RNA (el cual es más que todo ribosomal), pero incluye también carbohidratos, intermedios metabólicos y los "bloques de construcción" de las macromoléculas celulares tales como aminoácidos, nucleótidos y ácidos grasos. El componente D se compone de los constituyentes remanentes de las células típicas, los cuales son, principalmente, estructuras proteicas pero que también incluyen material genético (DNA).
La figura 1 ilustra las interacciones propuestas de las particiones R y D que simulan de forma simple, los procesos intracelulares correspondientes al crecimiento y al mantenimiento.
Figura 1.

Este modelo supone que la suma de las dos reacciones de describen la demanda de la fuente limitante de carbono y energía (S) (síntesis del componente R) y la formación del componente D; representa adecuadamente el crecimiento celular; y la inversión del componente D puede simular el metabolismo de mantenimiento. De esta forma, los miles de reacciones y procesos de transporte de masa que tienen lugar dentro de la célula o en las paredes y/o membranas, se agrupan dentro de estas tres simples conversiones.
De acuerdo con la tabla 1, se supone que la formación de R y D no es 100% eficiente como indican los coeficientes de rendimiento, YR y YD, respectivamente. La expresión para la síntesis de la partición D (principalmente polimerización de proteínas) juega el doble papel del componente R como fuente de reactivos (aminoácidos) y como catalizador (RNA ribosomal). La inversión del componente D, presumiblemente la degradación a aminoácidos o a constituyentes peptídicos (que no son procesos energéticos intensos), se representa con un rendimiento completo.
Tabla 1.
| Síntesis
de R: |
|
| Síntesis
de D: |
|
| Inversión
de D: |
A pesar de lo modesto de este modelo, se han obtenido impresionantes simulaciones del crecimiento de Klebsiella pneumoniae en glicerol, por parte de Esener et al. Sin embargo, la pendiente y el intercepto de una gráfica de xR, la concentración del componente R, contra m , no está de acuerdo con los valores experimentales. Se desea una correlación verificable experimentalmente dado que la concentración del componente R refleja cercanamente el contenido ribosomal, el cual es representativo de la capacidad de síntesis de proteínas. El problema se soluciona de forma simple, al sustraer una constante s , de xR en el término para la formación del componente D. Este ajuste refleja el incremento de ribosomas "inactivos" cuando la velocidad específica de crecimiento es baja, e incrementa el valor del intercepto del componente R (x0R) y disminuye la pendiente (m) correspondiente al perfil experimental.
Una sencilla ecuación de estado estacionario es suficiente para describir completamente la fase biótica, ya que xR y xD se suponen sumadas a la densidad constante de la fase biótica, rb. La ecuación que resulta (a partir del balance del componente R) es
1. |
Que incluye el término (m xR) que contabiliza la dilución del componente R del soporte debido al crecimiento celular. La velocidad específica de crecimiento puede expresarse en términos de yS y xR
2. |
La forma familiar del término de Michaelis – Menten de la demanda de sustrato (formación del componente R) sugiere una formulación simple de la ecuación de estado estado estacionario para describir el consumo y la difusión de nutriente. Sin embargo, la derivación de un balance para la difusión y la reacción con base en una concentración intrínseca de nutriente limitante, tiene algunas características que no son evidentes en las ecuaciones para la concentración del cultivo (no intrínseca). De otra parte, como el interior del biocatalizador está compuesto de cavidades (macroporos) densamente pobladas de células y una fracción inaccesible de "microporos", la construcción de la ecuación para la fase abiótica debería aproximarse a un problema difusional de dos fases. Esto es, la difusividad en el volumen relativamente pequeño entre las células en una microcolonia inmovilizada puede diferir significativamente de la que se encuentra en los "microporos" desocupados del soporte, debido al incremento de la tortuosidad o a la presencia de flujos poliméricos celulares.
La ecuación de estado estacionario para la fase abiótica (con base en el volumen abiótico) es
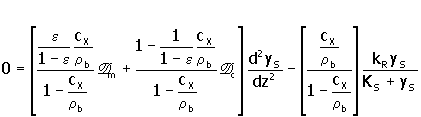 |
3. |
Donde, e es el volumen abiótico en las microcolonias inmovilizadas, y D m y D c son las difusividades del sustrato en las microcolonias y en el soporte desocupado, respectivamente. Esta ecuación se deriva con dos suposiciones. Primero, el flujo se supone unidireccional y sin componente convectivo. Segundo, la pseudoisotropía del biocatalizador interior se supone que permite el empleo del mismo gradiente de sustrato a lo largo de las microcolonias y los microporos del soporte.
La expresión dentro de los paréntesis cuadrados en el primer término de la ecuación inmediatamente anterior, realmente es un coeficiente de difusión compuesto, D m, una aproximación gruesa de las contribuciones combinadas al flujo (flux) difusivo de masa a través de las microcolonias y de los poros vacíos del soporte. El segundo término es simplemente la expresión para la demanda de sustrato, la cual depende del tamaño relativo de la fase biótica.
Obsérvese que el efecto final de ésta derivación sobre el término de demanda de sustrato equivale a la división por 1 – cX/rb. En las fermentaciones por lotes o quimiostáticas, cX/r b << 1, y, yS @ cS puesto que el volumen biótico es generalmente un pequeño porcentaje del volumen del cultivo. Por ello, la expresión para la demanda de sustrato se reduce a
4. |
y kR/r b constituye la velocidad constante comúnmente medida. Sin embargo, estas simplificaciones no pueden aplicarse a sistemas celulares viables inmovilizados ya que la fracción de volumen biótico es significativa. Con referencia a la relación 3, si se considera el caso simple en el cual D c = D m; la expresión dentro de los paréntesis cuadrados se reduce a D c obteniéndose
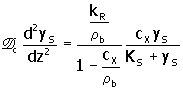 |
5. |
Aquí, la velocidad constante aparente difiere de la de un quimiostato en el factor 1/(1 – cX/r b). Obsérvese que la transformación de la ecuación 3 a la base usual, correspondiente al volumen total de catalizador [multiplicación por b (1 - cX/r b)] aun produce una velocidad constante aparente que difiere de la de un quimiostato en el factor b.
El análisis transiente es considerablemente más complejo, puesto que un término de la forma
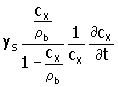 |
6. |
debe incluirse para contabilizar la concentración de sustrato en la fase abiótica debido a los cambios en el volumen de la fase biótica. Adicionalmente, la ecuación transiente de la fase abiótica se acopla a la ecuación de la fase biótica ya que la velocidad de cambio de cX con respecto al tiempo, depende de la velocidad de crecimiento así como del flujo (flux) de biomasa dentro del soporte. Con el fin de presentar el análisis de estado estable, en el cual cX se supone constante, una velocidad constante efectiva puede definirse como sigue
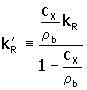 |
7. |
Las tres ecuaciones necesarias para modelar por completo el sistema descrito, se presentan en la tabla 2
Tabla 2.
| Fase abiótica (yS)
|
En yS
= ycS dyS/dz
= 0 En z = zS yS = ySS |
| Fase biótica (xR,
m)
|
|
| Pérdida de células (qSb)
|
|
La ecuación de pérdida de células define simplemente el flujo (flux) de biomasa en estado estacionario desde la superficie del soporte como la concentración de biomasa de la capa de células viables, cX multiplicada por la velocidad de crecimiento integrada sobre el espesor del soporte celular.
La solución de este sistema de ecuaciones se consigue de manera simple, por la integración de la ecuación de la fase abiótica una vez analíticamente, considerando la condición de frontera en la cual yS = y0S ó yS = ycS en la línea central de la capa de biocatalizador) y se resuelve numéricamente la ecuación de primer orden que resulta, con el uso, por ejemplo, del algoritmo de Runge – Kutta de cuarto orden. La concentración del componente R y la velocidad específica de crecimiento pueden calcularse en cada paso de integración para la evaluación conveniente de la integral que define la pérdida de células. Una lista completa de los valores de los parámetros investigados se incluye en la tabla 3
Tabla 3.
| Ecuación de la fase biótica | Ecuación de la fase abiótica |
| De Esener et al.: | |
| kR = 470,4 g/(l h) | D m = 3,5.10-6 cm2/s |
| km = 0,06 (l g)/h | D c = 7,0.10-6 cm2/s |
| YR = 0,73 | e = 0,20 |
| YD = 0,66 | cX/rb = 0,72 |
| KS = 0,07 g/l | ySS = 10,0 g/l |
| m = 48,7 (h g)/l | ycS = 1,393.10-3 g/l |
| x0R = 23,0 g/l | |
| De Maaløe y Kjeldgaard: | |
| rb = 240,0 g/l | |
| Calculados: | |
| kD = 0,0311 l/(g h) | |
| s = 20,1 g/l | |
| y0S = 1,393.10-3 g/l |