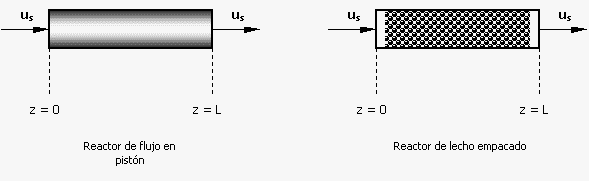
Reactores de flujo en pistón y de lecho empacado

El extremo opuesto al reactor de mezcla completa es el reactor de flujo en pistón, en el cual, el fluido se desplaza a lo largo de un tubo o canal de forma que se presenta un mezclado imperceptible en la dirección del flujo (la dirección axial), pero hay una mezcla bastante buena en la dirección radial. Tales reactores son comunes en la industria química, pero por razones que se considerarán más adelante, son poco utilizados para el crecimiento de células. Sin embargo, estos reactores se utilizan frecuentemente para células inmovilizadas y reacciones con enzimas. La isomerización de glucosa a fructosa, que es un paso clave en la producción de jarabe de maíz con un elevado contenido de fructosa, es un ejemplo importante de un proceso comercial que se lleva a cabo en un reactor de lecho de enzimas inmovilizadas. Los diagramas esquemáticos de un reactor de flujo en pistón y de uno de lecho empacado, se presentan a continuación:

Figura 1. Diagramas esquemáticos de un reactor de flujo en pistón y de uno de lecho empacado

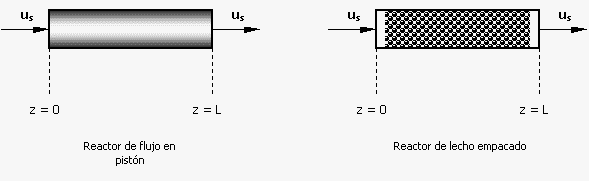
Considérese primero un reactor de flujo en pistón sin catalizador y que contiene células o una enzima. Si la velocidad superficial en la dirección axial (dirección z) es u_s (la velocidad superficial es la velocidad lineal promedio que el fluido debería tener si no hubiera empaque en el reactor y es igual a F/A , donde A es el área transversal del reactor y F es el flujo volumétrico dentro del mismo), se pueden escribir las siguientes ecuaciones de estado estacionario para el balance de células y de sustrato:

1.

Donde r_X y r_S son las velocidades de reacción basadas en los volúmenes de líquido.

Si la velocidad axial es constante, como debería ser el caso si la densidad del fluido permanece constante, estas ecuaciones se convierten en:

2.

Las cuales pueden reescribirse en función de un tiempo constante característico q (= z / u_s )

3.

Por consiguiente, las ecuaciones se reducen a las de un reactor por lotes, excepto que q reemplaza al tiempo t . Las condiciones iniciales y finales sobre las cuales estas ecuaciones se integran, son las siguientes:

Así, las soluciones para las ecuaciones anteriores para varias expresiones de velocidad (por ejemplo, la ecuación de Monod) pueden tomarse directamente de los resultados para un reactor por lotes.

El reactor de flujo en pistón ofrece un grado de conversión de sustrato mayor que el de un reactor de tanque agitado de igual volumen (y por lo tanto, igual tiempo de residencia), porque la velocidad de reacción en un reactor de tanque agitado será menor que en un reactor de flujo en pistón. En un reactor de tanque agitado, la concentración de sustrato cae inmediatamente al valor de salida y la velocidad de reacción se determina por este valor. Con una cinética del tipo Monod, la velocidad decrece al disminuir la concentración de sustrato; por ello, el reactor de flujo en pistón ofrece la ventaja de mayores velocidades de reacción que en un reactor de tanque agitado, debido a que la concentración de sustrato desciende desde su valor inicial a lo largo de la dirección axial.

Las principales dificultades en la operación de un reactor de flujo en pistón con células suspendidas radican en la necesidad de proveer un inóculo continuo de células (X₀ debe suministrarse a la entrada del reactor), y en el mantenimiento de un pH constante así como en el suministro de oxígeno a lo largo de la longitud del reactor. Estos problemas generalmente son tan extremos que existen pocos ejemplos de reactores biológicos perfectos de flujo en pistón. Algunos tipos de reactor pueden aproximarse como límite, al comportamiento de flujo en pistón; por ejemplo, un reactor con circulación pneumática de líquido con una fuerte circulación hacia arriba de líquido, o un gran tanque de tratamiento de aguas de desecho.

En contraste con el crecimiento microbial, los reactores de flujo en pistón y de lecho empacado se emplean comúnmente con enzimas libres e inmovilizadas. Aquí las necesidades de suministro de oxígeno y control de pH no se aplican usualmente, ya que muchas reacciones enzimáticas no requieren oxígeno y no generan ácidos o bases. Como se mencionó, una de las mayores aplicaciones industriales de este tipo es la isomerización de glucosa a fructosa para la producción de jarabe de maíz con alto contenido de fructosa. Esta reacción está catalizada por glucosa isomerasa inmovilizada sobre un soporte, tal como alúmina, en reactores de lecho empacado.

En un reactor de lecho empacado, la velocidad axial del fluido será mayor que en un reactor abierto de flujo en pistón y depende de la fracción de espacio vacío e , definida como:

y la velocidad de fluido intersticial, v_i , es:

La velocidad intersticial se emplea luego para calcular el tiempo de residencia del líquido t . Éste tiene el valor t = e (V/F ). En el caso de enzimas en solución, la fracción de espacio vacío e será igual a la unidad. Un valor típico de e para enzimas inmovilizadas sobre soportes esféricos es aproximadamente igual a 0,4. En el caso de enzimas libres o inmovilizadas, el balance de materia para el sustrato tiene la forma:

6.

y es posible la integración analítica de esta ecuación para algunas cinéticas comunes. La tabla 1 muestra ejemplos de la expresión del tiempo de residencia en función de los parámetros de la expresión de velocidad. Nótese que V'_M es el producto de V_M (máxima velocidad de reacción por unidad de volumen de catalizador -líquido más sólido-) y el volumen de catalizador por unidad de volumen de líquido (1-e )/e . De esta manera, V'_M = V_M(1-e )/e .

Tabla 1. Tiempo de residencia t en función de la conversión de sustrato [d = (c_S0 -c_S)/c_S0] para reacciones enzimáticas en reactores de flujo en pistón y de lecho empacado

Expresión de velocidad	Tiempo de residencia (t = e L/us )
Michaelis – Menten
Inhibición por sustrato
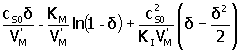