Correlaciones de transferencia de calor

La ecuación general de diseño de transferencia de calor es

1.

Se requiere una expresión para la coeficiente global de transferencia de calor U. Para la transferencia de calor en estado estable a través de una pared plana de espesor L_w , que separa la mezcla de fermentación a una temperatura T_{mezcla, 1} ; del fluido de calentamiento o enfriamiento o una temperatura T_{mezcla, 2} ; la continuidad del flujo de calor demanda

2.

Donde k_s en la conductividad térmica de la pared [kcal/(cm s ºC)]. En función del coeficiente global de transferencia de calor U, que se define por

3.

Organizando las ecuaciones anteriores se obtiene

Para una pared plana

4.

En clara analogía con la transferencia de masa, la resistencia global 1/U es la suma de las tres resistencias en serie. Para la transferencia de calor a través de la pared de un tubo cilíndrico, el área para la transferencia cambia continuamente a través de la pared. Para esta situación la ecuación apropiada para U es

Para la pared de un tubo

5.

Donde, d_i y d_o son los diámetros interior y exterior del tubo, respectivamente. El uso del subíndice o, para el coeficiente global de transferencia de calor, U, identifica la superficie exterior del tubo como el área base para la transferencia de calor. La conductividad térmica k_s del sólido depende del material y se incrementa ligeramente con una disminución de la temperatura. Los valores apropiados para diferentes materiales de transferencia de calor se encuentran en cualquier manual de ingeniería.

El análisis de transferencia de momento y de transferencia de calor de la interfase fluido – sólido, proporciona los coeficientes individuales de transferencia de calor (hw₁, hw₂) o (h_o, h_i) necesarios en las ecuaciones 4 y 5. Tales coeficientes varían a lo largo de la superficie de transferencia de calor, lo que obliga a la definición de un coeficiente global de transferencia de calor local, de acuerdo con las mismas ecuaciones 4 y 5. Se hace necesaria una detallada integración sobre el área de transferencia de calor para calcular el calor total transferido.

En general, para la transferencia de calor entre un fluido y una pared, los grupos adimensionales más importantes que se utilizan son:

Número de Nusselt

6.

Número de Prandlt

7.

Número de Reynolds

8.

Donde, k es la conductividad térmica del fluido; c_p es la capacidad calorífica, d es una distancia (diámetro o separación); m es la viscosidad y v la velocidad del fluido. Las variables sobre las que se definen estos números pueden variar ligeramente según sea la geometría del dispositivo de transferencia de calor.

El coeficiente de transferencia de calor, h, expresado adimensionalmente como el número de Nusselt, es función del número de Reynolds y del número de Prandlt

9.

Como la hidrodinámica puede variar de acuerdo a la forma de la superficie de intercambio; se puede disponer de correlaciones que incluyan la relación longitud, L, a diámetro, d, (L/d)

10.

Las variaciones de temperatura inducen variaciones en las propiedades del fluido en puntos diferentes cercanos a la superficie de intercambio. Como la viscosidad es la más importante de ellas, la relación

	Viscosidad del fluido a la temperatura media aritmética	11.
	Viscosidad del fluido a la temperatura de pared

Es una variable útil de correlación

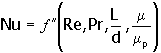12.

Como h (y por lo tanto Nu) puede definirse como un coeficiente local de transferencia de calor o como uno que se promedia sobre la superficie de transferencia de varias formas, se debe tener cuidado al determinar las temperaturas y las correlaciones para calcularlo.