Correlaciones para el coeficiente de transferencia de masa

El coeficiente de transferencia de masa se afecta por la configuración del fermentador y por las propiedades físicas del sistema gas – líquido. Generalmente las ecuaciones de transferencia de masa se expresan mediante grupos adimensionales que se obtienen por el método Pi de Buckingham a partir de las variables que influyen sobre el proceso. Los coeficientes y exponentes de las correlaciones obtenidas se deducen mediante el ajuste da datos experimentales.

La evidencia experimental indica que estas correlaciones son útiles para determinar el valor del coeficiente de transferencia de masa, K_l , y del coeficiente volumétrico de transferencia de masa, k_la , inclusive si los aspectos fundamentales de la mecánica de fluidos no aparecen explícitamente. La relación entre la potencia entregada al fluido y el volumen de la mezcla, P/V, probablemente incluye todos los efectos del número de Reynolds y de la viscosidad, si se tiene en cuenta que el consumo de potencia depende de cada fluido. La evaluación del coeficiente de transferencia de masa con el uso de correlaciones empíricas depende de las condiciones de operación y de la configuración del reactor empleado. Desgraciadamente muchas de las ecuaciones empíricas no informan sobre la constante de proporcionalidad o sobre las condiciones de operación utilizadas en los diferentes ensayos realizados para su deducción, situación que limita su uso.

El coeficiente volumétrico de transferencia de masa, k_la, es la combinación de dos parámetros experimentales, el coeficiente de transferencia de masa, k_l , y el área de la superficie de separación gas – líquido (o área interfacial)

Y, a, se calcula de la siguiente forma

Donde, y es la fracción volumétrica de gas en la fase dispersa (retención de gas -holdup-); D₃₂ es el diámetro medio de Sauter

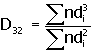Donde, h_A es la altura ocupada por el líquido aireado; h₀ es la altura del líquido sin airear; n es el número de burbujas; d_i es el diámetro de las burbujas.

La fracción volumétrica del gas en la fase dispersa, conocida también como retención de gas, depende principalmente de la velocidad superficial del gas y del consumo de potencia. En algunos casos el gas provee por sí mismo la agitación del líquido, pero con mayor frecuencia se utiliza un impulsor, preferencialmente tipo turbina, para dispersar el gas y hacer circular la dispersión líquido – gas a través del reactor. La retención de gas es uno de los parámetros más sensibles a las propiedades físicas del líquido.

Calderbank y Moo – Young, (1961), presentan las siguientes ecuaciones, confirmadas por Calderbank y Jones (1961), para evaluar el coeficiente de transferencia de masa en dispersiones gas – líquido con partículas sólidas de baja densidad en reactores agitados. Las partículas simulan la transferencia de masa entre burbujas con un diámetro menor a 2,5 mm y los microorganismos en un fermentador

Para burbujas con un diámetro mayor a 2,5 mm

Donde, K_l es el coeficiente global de transferencia de masa (m/s); Sh es el número de Sherwood; Sc es el número de Schmidt; Gr es el número de Grashof; D₃₂ es el diámetro medio de Sauter (m); D _AB es la difusividad del componente A en el componente B (m²/s); m_c es la viscosidad de la fase continua [kg/(m/s)]; r_c es la densidad de la fase continua (kg/m³); g es la aceleración de la gravedad; Dr es la diferencia de densidades entre el líquido y el gas.

Van’t Riet (1979), presenta la siguiente ecuación para evaluar la transferencia de oxígeno en agua en reactores agitados mecánicamente, cuyo volumen está entre 2 y 2600 litros

Donde, k_la es el coeficiente volumétrico de transferencia de masa (1/s), calculado con una aproximación entre 20 y 40%; P es la potencia entregada al fluido (W); V es el volumen de la mezcla en el fermentador (m³); v_s es la velocidad superficial del aire, v_s = Q/A (m/s); Q es el caudal de gas (m³/s); A es el área transversal, A = (p /4)D²_T (m²); D_T es el diámetro del fermentador (m).

Van’ Riet (1979), recomienda la siguiente ecuación para evaluar k_la con una aproximación entre 20 y 40%, en el caso de la transferencia de oxígeno en soluciones de electrolitos fuertes, no coalescentes, en fermentadores agitados mecánicamente, cuyo volumen varía entre 2 y 4400 litros

Las dos ecuaciones anteriores se aplican a reactores provistos con diversos tipos de agitadores, diferentes relaciones entre el diámetro del impulsor y el diámetro del tanque; y una relación entre la potencia disipada por el impulsor y el volumen de la mezcla, (P/V) entre 500 y 10000 (W/m³).

Humphrey (1977), recomienda las siguientes ecuaciones para evaluar k_la, en tanques agitados mecánicamente según el volumen del fermentador

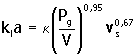Al nivel de planta piloto

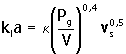En plantas de producción

Donde, k es una constante que depende de la configuración del sistema y del sistema de unidades empleado.

Akita y Yoshida (1973), presentan la siguiente ecuación para calcular el coeficiente de transferencia de oxígeno en diferentes soluciones acuosas en columnas de burbujeo

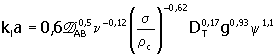Donde, D _AB es la difusividad de A en B, (m²/s); n es la viscosidad cinemática de la mezcla (m²/s); s es la tensión superficial (N/m); r_c es la densidad de la mezcla (kg/m³); D_T es el diámetro del tanque (m); g es la aceleración de la gravedad; y es la fracción volumétrica del gas en la fase dispersa (adimensional).