1.
Consumo de sustrato de acuerdo con la cinética de Michaelis – Menten
La velocidad de consumo de sustrato, si se supone que la cinética intrínseca de la reacción local de la enzima inmovilizada se comporta según la ecuación de Michaelis – Menten, es
1. |
Con VM = e r q
Donde, VM es la velocidad máxima de la reacción; e es la actividad de la enzima inmovilizada, (m moles sustrato convertido)(tiempo)-1(m moles enzima)-1; r es la densidad del soporte, (masa del soporte)/(volumen del soporte); q es la carga de la enzima (m moles enzima)/(masa del soporte)
Si se reemplaza la ecuación 1 en la ecuación de balance de materiales y se expresa el resultado en forma adimiensional, se obtiene
2. |
Con x = cS/co; b = co/KM; t = R/Ro
Donde, Ro es el radio de la partícula esférica que sirve como soporte, y f es el módulo de Thiele, definido por:
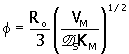 |
3. |
Las condiciones de frontera asociadas con la ecuación 2 son
4. |
Estas condiciones expresadas en forma adimensional se transforman en
5. |
Donde, Rc es el radio crítico, en el cual la concentración de sustrato es igual a cero.
La velocidad global de consumo de sustrato en una partícula esférica con enzimas inmovilizadas es
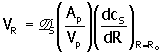 |
6. |
Donde, VR es la velocidad observada de consumo de sustrato; Ap/Vp es la relación entre el área superficial y el volumen de la partícula, que para el caso de partículas esféricas es igual a 3/Ro.
La ecuación 6 expresada en forma adimensional se convierte en
7. |
La ecuación 1 expresada en forma adimensional es
8. |
Donde, Vo es la velocidad de la reacción correspondiente a la concentración de sustrato co, prevaleciente en el seno del fluido; b = co/KM
9. |
La velocidad máxima de reacción, expresada en función del modulo de Thiele es
10. |
La velocidad de la reacción si no hubiera resistencia a la transferencia de masa, se obtiene mediante el reemplazo de VM de la ecuación 10 en la ecuación 8
11. |
El factor de efectividad,h, se define como la relación entre la velocidad real de la reacción (ecuación 7) y la velocidad de la reacción si no hubiera resistencia a la transferencia de masa (ecuación 11)
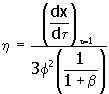 |
12. |